HHL算法的目标

求解\(A\vec{x}=\vec{b}\)，其中\(A\)是\(n\times n\)的方阵，\(\vec{x}\)和\(\vec{b}\)都是\(n\times1\)的向量。假设矩阵\(A\)是厄密的（即\(A^{\dagger}=A\)），则矩阵\(e^{iAt}\)是酉的（即\(AA^{\dagger}=A^{\dagger}A=I\)），同时\(A\)和\(e^{iAt}\)有相同的特征向量，若\(A|u\rangle=\lambda|u\rangle\)，则\(e^{iAt}|u\rangle=e^{i\lambda t}|u\rangle\)。本问题中，还需假设\(\|\vec{x}\|=1,\|\vec{b}\|=1\)。因为\(e^{iAt}\)是酉矩阵，所以它有\(n\)个相互正交的特征向量。本问题中，将问题变形为\(A|x\rangle=|b\rangle\)，并不完全等同于原问题。

很多地方笔者并没有完全搞懂，故省略了很多推导过程和证明，后面可能会补充。

HHL算法的量子线路图

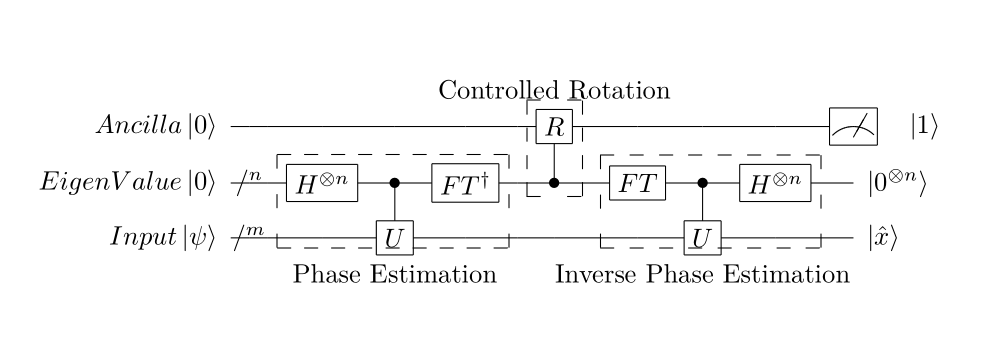
其对应的latex代码为：

\documentclass{article}
\usepackage[]{qcircuit}
\usepackage{ifpdf}
\xyoption{all}
\newcommand{\ket}[1]{\ensuremath{\left\vert #1 \right\rangle}}
\newcommand{\bra}[1]{\ensuremath{\left\langle{#1}\right\vert}}
\begin{document}
	\Qcircuit@C=0.7em@R=0.7em {
		&          &                        &        &                   &   &         &\mbox{Controlled Rotation} \\
		\lstick{Ancilla \ket{0}}   &\qw       &\qw&\qw                 &\qw     &\qw                &\qw&\gate{R} &\qw&\qw      &\qw     &\qw                 &\meter&\rstick{\ket{1}} \\
		\lstick{EigenValue \ket{0}}&\qw{/^{n}}&\qw&\gate{H^{\otimes n}}&\ctrl{1}&\gate{FT^{\dagger}}&\qw&\ctrl{-1}&\qw&\gate{FT}&\ctrl{1}&\gate{H^{\otimes n}}&\rstick{\ket{0^{\otimes n}}}\qw \\
		\lstick{Input \ket{\psi}}  &\qw{/^{m}}&\qw&\qw                 &\gate{U}&\qw                &\qw&\qw      &\qw&\qw      &\gate{U}&\qw&\rstick{\ket{\hat{x}}}\qw 
		\gategroup{3}{4}{4}{6}{.7em}{--}  \gategroup{2}{8}{3}{8}{.7em}{--} \gategroup{3}{10}{4}{12}{.7em}{--}\\
		&&&&\mbox{Phase Estimation}&&&&&&\mbox{Inverse Phase Estimation}
	}
\end{document}

相位估计算法(Quantum phase estimation)

量子逆傅里叶变换(逆QFT)

数学形式：\(f(j)=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}\hat{f}(k)\exp(-2\pi ijk/N),\, j=0,1,\ldots,N-1\)

量子态形式：\(|\psi\rangle=\mathcal{F}^{-1}(|\hat{\psi}\rangle),\, |\hat{\psi}\rangle=\sum_{k=0}^{2^{n}-1}\hat{f}(k)|k\rangle,\, |\psi\rangle=\sum_{j=0}^{2^{n}-1}f(j)|j\rangle,\, 2^{n}=N\)

若\(\mathcal{F}^{-1}(|k\rangle)=\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}\exp(-2\pi ijk/2^{n})|j\rangle\)，则 \[ \begin{equation} \begin{aligned} |\psi\rangle & =\mathcal{F}^{-1}(|\hat{\psi}\rangle) \\ & =\sum_{k=0}^{2^{n}-1}\hat{f}(k)\mathcal{F}^{-1}(|k\rangle) \\ & =\frac{1}{\sqrt{2^{n}}}\sum_{k=0}^{2^{n}-1}\hat{f}(k)\sum_{j=0}^{2^{n}-1}\exp(-2\pi ijk/2^{n})|j\rangle \\ & =\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}(\sum_{k=0}^{2^{n}-1}\hat{f}(k)\exp(-2\pi ijk/2^{n}))|j\rangle \\ & =\sum_{j=0}^{2^{n}-1}f(j)|j\rangle \end{aligned} \end{equation} \]

所以，逆QFT为：\(\mathcal{F}^{-1}(|k\rangle)=\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}\exp(-2\pi ijk/2^{n})|j\rangle\)

离散傅里叶变换(DFT)

对于N点序列\(\{x[n]\},0\leq n<N\)，其DFT为：\(\hat{x}[k]=\sum_{n=0}^{N-1}e^{-i\frac{2\pi}{N}nk}x[n],k=0,1,\ldots,N-1\)，记为\(\hat{x}=\mathcal{F}\{x\}\)，其逆DFT为：\(x[n]=\frac{1}{N}\sum_{k=0}^{N-1}e^{i\frac{2\pi}{N}nk}\hat{x}[k],n=0,1,\ldots,N-1\)，记为\(x=\mathcal{F}^{-1}\{\hat{x}\}\)。

将DFT和逆DFT两个式子的两边分别乘\(\sqrt{N}\)，得\((\sqrt{N}\hat{x}[k])=\sum_{n=0}^{N-1}e^{-i\frac{2\pi}{N}nk}(\sqrt{N}x[n]),k=0,1,\ldots,N-1\)与\((\sqrt{N}x[n])=\frac{1}{N}\sum_{k=0}^{N-1}e^{i\frac{2\pi}{N}nk}(\sqrt{N}\hat{x}[k]),n=0,1,\ldots,N-1\)。

整理可得：\(\hat{x}[k]=\frac{1}{\sqrt{N}}\sum_{n=0}^{N-1}e^{-i\frac{2\pi}{N}nk}(\sqrt{N}x[n]),k=0,1,\ldots,N-1\)与\((\sqrt{N}x[n])=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{i\frac{2\pi}{N}nk}\hat{x}[k],n=0,1,\ldots,N-1\)。

换元可得：逆DFT：\(x_{k}=\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}y_{j}e^{-2\pi ijk/N}\)与DFT：\(y_{k}=\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}x_{j}e^{2\pi ijk/N}\)，其中\(k=0,1,\ldots,N-1\)。

量子傅里叶变换(QFT)

即用量子线路实现DFT：\(\hat{f}(k)=\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}f(j)e^{2\pi ijk/N},\, k=0,1,\ldots,N-1\)。

用量子态表示DFT为：\(|\hat{\psi}\rangle=\mathcal{F}(|\psi\rangle),\, |\hat{\psi}\rangle=\sum_{k=0}^{2^{n}-1}\hat{f}(k)|k\rangle,\, |\psi\rangle=\sum_{j=0}^{2^{n}-1}f(j)|j\rangle,\, 2^{n}=N\)。

若\(\mathcal{F}(|j\rangle)=\frac{1}{\sqrt{2^{n}}}\sum_{k=0}^{2^{n}-1}e^{2\pi ijk/2^{n}}|k\rangle\)，则

\[ \begin{equation} \begin{aligned} |\hat{\psi}\rangle & = \mathcal{F}(|\psi\rangle) \\ & =\sum_{j=0}^{2^{n}-1}f(j)\mathcal{F}(|j\rangle) \\ &=\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n-1}}f(j)\sum_{k=0}^{2^{n}-1}\exp(2\pi ijk/2^{n})|k\rangle \\ & =\frac{1}{\sqrt{2^{n}}}\sum_{k=0}^{2^{n}-1}(\sum_{j=0}^{2^{n}-1}\exp(2\pi ijk/2^{n})f(j)) |k\rangle \\ & =\sum_{k=0}^{2^{n}-1}\hat{f}(k)|k\rangle \end{aligned} \end{equation} \]

所以QFT为：\(\mathcal{F}(|j\rangle)=\frac{1}{\sqrt{2^{n}}}\sum_{k=0}^{2^{n}-1}e^{2\pi ijk/2^{n}}|k\rangle\)。

Deutsch算法

假设某函数\(f(x)\)，它的定义域是\(\{0,1\}^n\) ，即是长度为\(n\)的01串，它的值域是\(\{0,1\}\)。而且它只可能是两种，一种是常数函数 ，即$x,f(x)=c,c{0,1} \(；另一种是平衡函数，即有一半的x，使得\)f(x)=0\(，有另一半\)x\(，使得\)f(x)=1\(。问题就是判断\)f(x)$是常数函数还是平衡函数。

传统算法：至少需要\(2^{n-1}+1\)次操作，假设验证了\(2^{n-1}+1\)个\(f(x)\)的值后，都是某一常数c(\(c\in \{0,1\}\))，则可知\(f(x)\)是常数函数，否则是平衡函数。

量子算法：用Deutsch算法来判断，仅需一次操作即可知\(f(x)\)是常数函数还是平衡函数。

算法线路图：

上边输入为\(|0\rangle^{\otimes n}\)，下边输入为\(|1\rangle\)。

\[ |\psi_{0}\rangle=|0\rangle^{\otimes n}|1\rangle \]

\[ H^{\otimes n}|x\rangle=\prod_{i=1}^{n}\frac{1}{\sqrt{2}}\sum_{y_{j}\in \{0,1\}}(-1)^{x_{i}y_{j}}|y_{j}\rangle=\frac{1}{2^{n/2}}\sum_{y=0}^{2^{n}-1}(-1)^{x\cdot y}|y\rangle \]

其中，\(x\cdot y=x_{1}y_{1}\oplus x_{2}y_{2}\oplus\cdots\oplus x_{n}y_{n}\)

\[ H^{\otimes n}|0\rangle = \sum_{x=0}^{2^{n}-1}\frac{|x\rangle}{\sqrt{2^{n}}} \] 所以\(|\psi_{1}\rangle=\sum_{x=0}^{2^{n}-1}\frac{|x\rangle}{\sqrt{2^{n}}}\cdot\frac{|0\rangle -|1\rangle}{\sqrt{2}}\)

经过\(U_{f}\)的作用后，\(x\)保持不变，\(y\)变为\(y\oplus f(x)\)。因为\(y=\frac{|0\rangle -|1\rangle}{\sqrt{2}}\)，所以\(y\oplus f(x)=\frac{1}{\sqrt{2}}(|f(x)\rangle-|1\oplus f(x)\rangle)\)。当\(f(x)=0\)时，\(y\oplus f(x)=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\)；当\(f(x)=1\)时，\(y\oplus f(x)=\frac{1}{\sqrt{2}}(|1\rangle-|0\rangle)=-\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\)。所以\(y\oplus f(x)=(-1)^{f(x)}|y\rangle\)。

所以\(|\psi_{2}\rangle=\sum_{x=0}^{2^{n}-1}\frac{(-1)^{f(x)}}{\sqrt{2^{n}}}|x\rangle\cdot\frac{|0\rangle-|1\rangle}{\sqrt{2}}\)。

再经过一次Hadamard变换，\(|\psi_{3}\rangle=\frac{1}{2^{n}}\sum_{x=0}^{2^{n}-1}(-1)^{f(x)}\sum_{y=0}^{2^{n}-1}(-1)^{x\cdot y}|y\rangle\cdot\frac{|0\rangle-|1\rangle}{\sqrt{2}}=\frac{1}{2^{n}}\sum_{x=0}^{2^{n}-1}\sum_{y=0}^{2^{n}-1}(-1)^{f(x)+x\cdot y}|y\rangle \cdot\frac{|0\rangle-|1\rangle}{\sqrt{2}}\)。

然后只需测量上边部分，如果测量结果为\(|0\rangle^{\otimes n}\)，则是常数函数，否则是对称函数。