HHL算法(量子求解线性方程组)
HHL算法的目标
求解\(A\vec{x}=\vec{b}\),其中\(A\)是\(n\times n\)的方阵,\(\vec{x}\)和\(\vec{b}\)都是\(n\times1\)的向量。假设矩阵\(A\)是厄密的(即\(A^{\dagger}=A\)),则矩阵\(e^{iAt}\)是酉的(即\(AA^{\dagger}=A^{\dagger}A=I\)),同时\(A\)和\(e^{iAt}\)有相同的特征向量,若\(A|u\rangle=\lambda|u\rangle\),则\(e^{iAt}|u\rangle=e^{i\lambda t}|u\rangle\)。本问题中,还需假设\(\|\vec{x}\|=1,\|\vec{b}\|=1\)。因为\(e^{iAt}\)是酉矩阵,所以它有\(n\)个相互正交的特征向量。本问题中,将问题变形为\(A|x\rangle=|b\rangle\),并不完全等同于原问题。
很多地方笔者并没有完全搞懂,故省略了很多推导过程和证明,后面可能会补充。
HHL算法的量子线路图
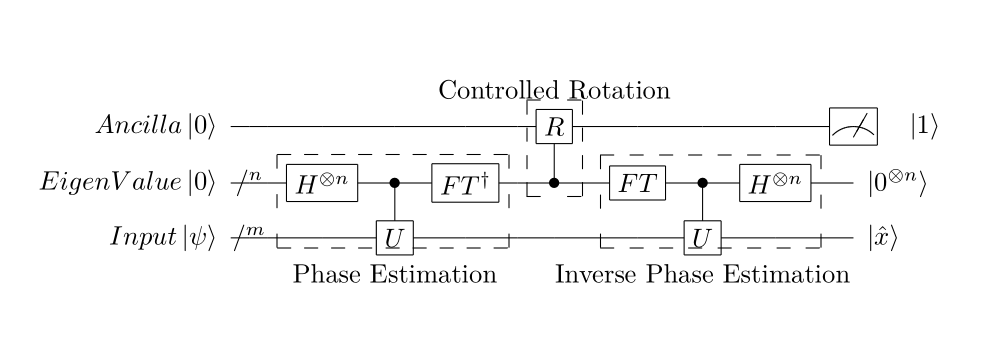
其对应的latex代码为:
\documentclass{article}
\usepackage[]{qcircuit}
\usepackage{ifpdf}
\xyoption{all}
\newcommand{\ket}[1]{\ensuremath{\left\vert #1 \right\rangle}}
\newcommand{\bra}[1]{\ensuremath{\left\langle{#1}\right\vert}}
\begin{document}
\Qcircuit@C=0.7em@R=0.7em {
& & & & & & &\mbox{Controlled Rotation} \\
\lstick{Ancilla \ket{0}} &\qw &\qw&\qw &\qw &\qw &\qw&\gate{R} &\qw&\qw &\qw &\qw &\meter&\rstick{\ket{1}} \\
\lstick{EigenValue \ket{0}}&\qw{/^{n}}&\qw&\gate{H^{\otimes n}}&\ctrl{1}&\gate{FT^{\dagger}}&\qw&\ctrl{-1}&\qw&\gate{FT}&\ctrl{1}&\gate{H^{\otimes n}}&\rstick{\ket{0^{\otimes n}}}\qw \\
\lstick{Input \ket{\psi}} &\qw{/^{m}}&\qw&\qw &\gate{U}&\qw &\qw&\qw &\qw&\qw &\gate{U}&\qw&\rstick{\ket{\hat{x}}}\qw
\gategroup{3}{4}{4}{6}{.7em}{--} \gategroup{2}{8}{3}{8}{.7em}{--} \gategroup{3}{10}{4}{12}{.7em}{--}\\
&&&&\mbox{Phase Estimation}&&&&&&\mbox{Inverse Phase Estimation}
}
\end{document}HHL的算法解释
第一步:相位估计(Phase Estimation)
首先,有\(|b\rangle=\sum_{i=0}^{N-1}b_{i}|i\rangle=\sum_{i=0}^{N-1}\beta_{i}|\mu_{i}\rangle\),其中\(\mu_{i}\)是\(A\)(和\(e^{iAt}\))的特征向量。然后,因为\(U=e^{iAt}\)是酉的,故可以用Hamiltonian simulation来制备\(U\)门。
相位估计的电路图和功能如下:
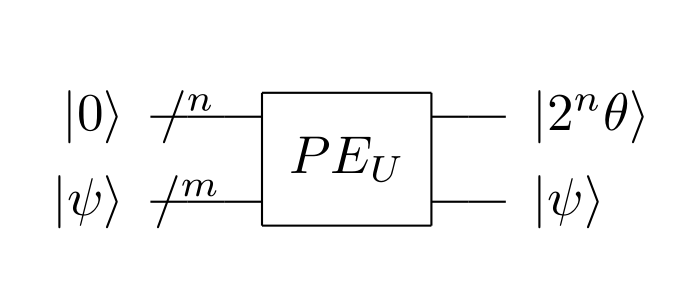
其对应的latex代码为:
\documentclass{article}
\usepackage[]{qcircuit}
\usepackage{ifpdf}
\xyoption{all}
\newcommand{\ket}[1]{\ensuremath{\left\vert #1 \right\rangle}}
\newcommand{\bra}[1]{\ensuremath{\left\langle{#1}\right\vert}}
\begin{document}
\Qcircuit@C=0.7em@R=0.7em {
\lstick{\ket{0}} &\qw{/^{n}}&\qw&\multigate{1}{PE_{U}}&\qw&\rstick{\ket{2^{n}\theta}}\qw \\
\lstick{\ket{\psi}}&\qw{/^{m}}&\qw&\ghost{PE_{U}} &\qw&\rstick{\ket{\psi}}\qw
}
\end{document}具体的实现方式见我的另一篇文章。
相位估计中,\(|\psi\rangle\)是\(U\)的特征向量,\(U|\psi\rangle=e^{2\pi i\theta}|\psi\rangle\)。输出得到\(|2^{n}\theta\rangle\)。本文中,\(U=e^{iAt}\),若\(A|\psi\rangle=\lambda|\psi\rangle\),则\(U|\psi\rangle=e^{i\lambda t}|\psi\rangle\)。因此,在相位估计后,若Eigenvalue的值变为\(|\hat{\lambda}\rangle\),则\(\hat{\lambda}=2^{n}\frac{\lambda t}{2\pi}\)。因此\(\hat{\lambda}\)与\(\lambda\)是正比关系。后面就认为\(\hat{\lambda}\)是对\(\lambda\)的估计。
相位估计之前,\(|\psi\rangle=\sum_{i=0}^{N-1}\beta_{i}|\mu_{i}\rangle\),因此相位估计后,Input与Eigenvalue变为\(\sum_{j=0}^{N-1}\beta_{j}|\mu_{j}\rangle|\lambda_{j}\rangle\)。
第二步:受控旋转,所有的Qubits变为\(\sum_{j=0}^{N-1}\beta_{j}|\mu_{j}\rangle|\lambda_{j}\rangle(\sqrt{1-\frac{C^{2}}{\lambda_{j}}}|0\rangle+\frac{C}{\lambda}|1\rangle)\)。
第三步:逆相位估计,得到\(\sum_{j=0}^{N-1}\beta_{j}|\mu_{j}\rangle|0\rangle(\sqrt{1-\frac{C^{2}}{\lambda_{j}}}|0\rangle+\frac{C}{\lambda}|1\rangle)\)
第四步:对Ancilla进行测量,当得到\(|1\rangle\)的时候,Input变为\(|\hat{x}\rangle=\frac{1}{N_{x'}}\sum_{j=0}^{N-1}\frac{C}{\lambda_{j}}\beta_{j}|\mu_{j}\rangle\),与我们想要的\(|x\rangle=\sum_{j=0}^{N-1}\beta_{j}\frac{1}{\lambda_{j}}|\mu_{j}\rangle\)成正比关系,故相当于得到了\(|x\rangle\)。
相关证明
- \(A\)是厄密矩阵,所以\(A\)有\(n\)个相互正交的特征向量,证明\(e^{iAt}\)是酉矩阵。因为A是Hermitian矩阵,所以存在酉矩阵\(U\),使得\(D=U^{\dagger}AU\)为实对角阵。由矩阵级数的定义可知,\(U^{\dagger}e^{iA}U=e^{iU^{\dagger}AU}=e^{iD}\),因为\(D\)是实对角阵,所以\(e^{iD}\)也是实对角阵,特征值形如\(e^{i\lambda}\),其中\(\lambda\)是实数(\(D\)的对角元,\(A\)的特征值)。由欧拉公式可得\(e^{i\lambda}=\cos\lambda+i\sin\lambda\),其复共轭为\(\cos\lambda-i\sin\lambda=e^{-i\lambda}\),所以\(e^{iD}\times e^{-iD}=E\),所以\(e^{iD}\)是酉矩阵。所以\(e^{iA}=Ue^{iD}U^{\dagger}\)也是酉矩阵。