量子相位估计算法
相位估计算法(Quantum phase estimation)
量子逆傅里叶变换(逆QFT)
数学形式:\(f(j)=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}\hat{f}(k)\exp(-2\pi ijk/N),\, j=0,1,\ldots,N-1\)
量子态形式:\(|\psi\rangle=\mathcal{F}^{-1}(|\hat{\psi}\rangle),\, |\hat{\psi}\rangle=\sum_{k=0}^{2^{n}-1}\hat{f}(k)|k\rangle,\, |\psi\rangle=\sum_{j=0}^{2^{n}-1}f(j)|j\rangle,\, 2^{n}=N\)
若\(\mathcal{F}^{-1}(|k\rangle)=\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}\exp(-2\pi ijk/2^{n})|j\rangle\),则 \[ \begin{equation} \begin{aligned} |\psi\rangle & =\mathcal{F}^{-1}(|\hat{\psi}\rangle) \\ & =\sum_{k=0}^{2^{n}-1}\hat{f}(k)\mathcal{F}^{-1}(|k\rangle) \\ & =\frac{1}{\sqrt{2^{n}}}\sum_{k=0}^{2^{n}-1}\hat{f}(k)\sum_{j=0}^{2^{n}-1}\exp(-2\pi ijk/2^{n})|j\rangle \\ & =\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}(\sum_{k=0}^{2^{n}-1}\hat{f}(k)\exp(-2\pi ijk/2^{n}))|j\rangle \\ & =\sum_{j=0}^{2^{n}-1}f(j)|j\rangle \end{aligned} \end{equation} \]
所以,逆QFT为:\(\mathcal{F}^{-1}(|k\rangle)=\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}\exp(-2\pi ijk/2^{n})|j\rangle\)
逆QFT的张量积形式
定义\(k\)的二进制表示,\(k=k_{n-1}k_{n-2}\ldots k_{0}=k_{n-1}2^{n-1}+k_{n-2}2^{n-2}+\ldots +k_{0}2^{0}\),对于小数来说,\(0.k_{l}k_{l+1}\ldots k_{m}=\frac{1}{2}k_{l}+\frac{1}{2^{2}}k_{l+1}+\ldots +\frac{1}{2^{m-l+1}}k_{m}\)。 \[ \begin{equation} \begin{aligned} \mathcal{F}^{-1}(|k\rangle)& =\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}\exp(-2\pi ijk/2^{n})|j\rangle \\ & =\frac{1}{\sqrt{2^{n}}}\sum_{j_{n-1}=0}^{1}\ldots\sum_{j_{0}=0}^{1}\exp(-2\pi ik\sum_{l=1}^{n}\frac{j_{n-l}}{2^{l}})|j_{n-1}\ldots j_{0}\rangle \\ & =\frac{1}{\sqrt{2^{n}}}\sum_{j_{n-1}=0}^{1}\ldots\sum_{j_{0}=0}^{1}\otimes_{l=1}^{n}\exp(-2\pi ik\frac{j_{n-l}}{2^{l}})|j_{n-l}\rangle \\ & =\frac{1}{\sqrt{2^{n}}}\otimes_{l=1}^{n}[\sum_{j_{n-l}=0}^{1}\exp(-2\pi ik\frac{j_{n-l}}{2^{l}})|j_{n-l}\rangle] \\ & =\frac{1}{\sqrt{2^{n}}}\otimes_{l=1}^{n}[|0\rangle+\exp(-2\pi ik\frac{1}{2^{l}})|1\rangle] \\ & =\frac{1}{\sqrt{2^{n}}}(|0\rangle+e^{-2\pi i0.k_{0}}|1\rangle)\otimes(|0\rangle+e^{-2\pi i0.k_{1}k_{0}}|1\rangle)\otimes\ldots\otimes(|0\rangle+e^{-2\pi i0.k_{n-1}k_{n-2}\ldots k_{0}}|1\rangle) \end{aligned} \end{equation} \]
逆QFT的量子线路模型
假设量子门\(R_{k}^{\dagger}=\begin{bmatrix}1&0\\0&\exp(\frac{-2\pi i}{2^{k}})\end{bmatrix}\),与QFT类似可得逆QFT的量子线路图。
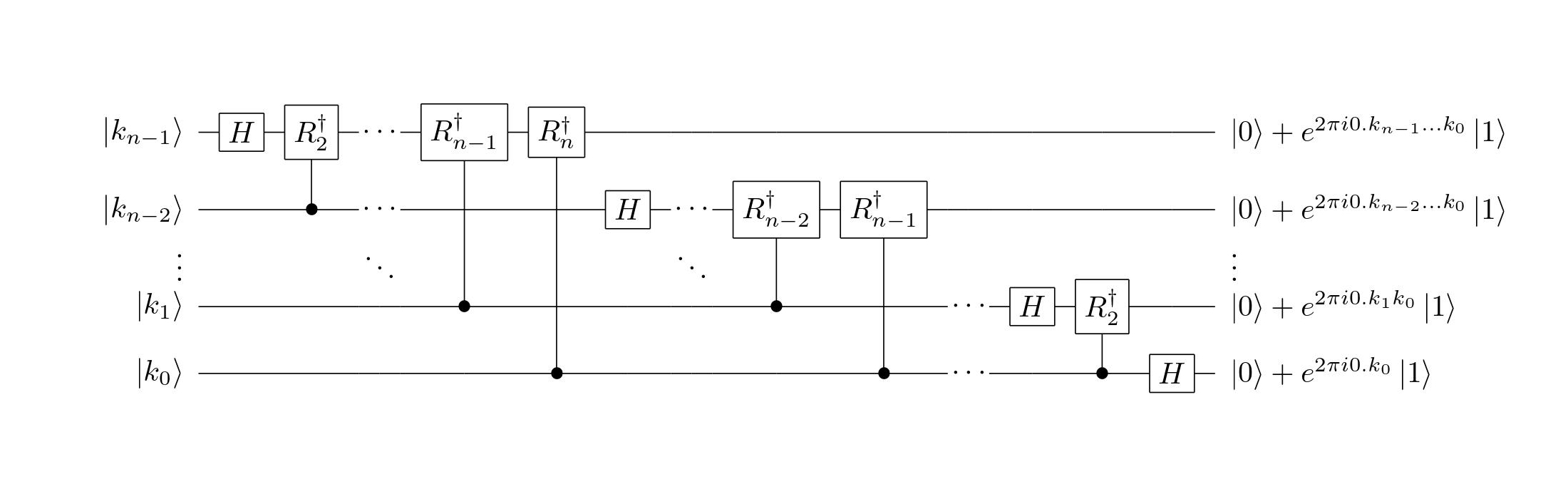
其latex代码为:
\documentclass{article}
\usepackage[]{qcircuit}
\usepackage{ifpdf}
\xyoption{all}
\newcommand{\ket}[1]{\ensuremath{\left\vert #1 \right\rangle}}
\newcommand{\bra}[1]{\ensuremath{\left\langle{#1}\right\vert}}
\begin{document}
\Qcircuit@C=0.7em@R=0.7em {
\lstick{\ket{k_{n-1}}}&\gate{H}&\gate{R_{2}^{\dagger}}&\qw&\cdots& &\gate{R_{n-1}^{\dagger}}&\gate{R_{n}^{\dagger}}&\qw &\qw&\qw &\qw&\qw &\qw &\qw&\qw &\qw&\qw &\qw &\qw &\rstick{\ket{0}+e^{2\pi i0.k_{n-1}\ldots k_{0}}\ket{1}}\qw \\
\lstick{\ket{k_{n-2}}}&\qw &\ctrl{-1} &\qw&\cdots& &\qw &\qw &\gate{H}&\qw&\cdots& &\gate{R_{n-2}^{\dagger}}&\gate{R_{n-1}^{\dagger}}&\qw&\qw &\qw&\qw &\qw &\qw &\rstick{\ket{0}+e^{2\pi i0.k_{n-2}\ldots k_{0}}\ket{1}}\qw \\
\lstick{\vdots} & & & &\ddots& & & & & &\ddots& & & & & & & & & &\rstick{\vdots} \\
\lstick{\ket{k_{1}}} &\qw &\qw &\qw&\qw &\qw&\ctrl{-3} &\qw &\qw &\qw&\qw &\qw&\ctrl{-2} &\qw &\qw&\cdots& &\gate{H}&\gate{R_{2}^{\dagger}}&\qw &\rstick{\ket{0}+e^{2\pi i0.k_{1}k_{0}}\ket{1}}\qw \\
\lstick{\ket{k_{0}}} &\qw &\qw &\qw&\qw &\qw&\qw &\ctrl{-4} &\qw &\qw&\qw &\qw&\qw &\ctrl{-3} &\qw&\cdots& &\qw &\ctrl{-1} &\gate{H}&\rstick{\ket{0}+e^{2\pi i0.k_{0}}\ket{1}}\qw
}
\end{document}量子相位估计
假设某一酉算符\(U\),它的本征态是\(|\psi\rangle\),且\(U|\psi\rangle=\lambda|\psi\rangle\),即\(|\psi\rangle\)对应的本征值是\(\lambda\)。量子相位估计即是估计\(\lambda\),不妨假设\(\lambda=\exp 2\pi i\theta\),估计\(\theta\)即可估计\(\lambda\)。由于\(U^{\dagger}U=I\)(\(U\)是酉矩阵),所以\(\langle\psi|U^{\dagger}U|\psi\rangle=\langle\psi|\psi\rangle\),\(\langle\psi|U^{\dagger}U|\psi\rangle=\langle\psi|\lambda^{*}\lambda|\psi\rangle=|\lambda|^{2}\langle\psi|\psi\rangle\),所以\(|\lambda|^{2}=1\)。故可设\(\lambda=\exp(2\pi i\theta),0\leq\theta<1\),所以,通过估计\(\theta\)即可估计\(\lambda\)。
其线路模型如下:
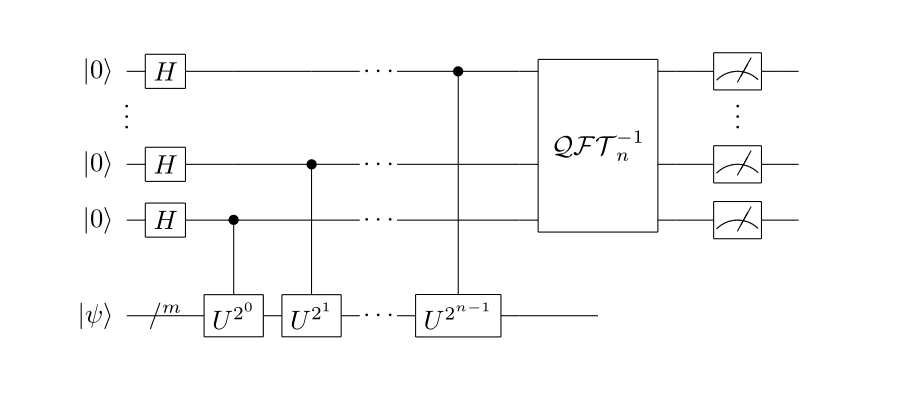
对应latex代码为:
\documentclass{article}
\usepackage[]{qcircuit}
\usepackage{ifpdf}
\xyoption{all}
\newcommand{\ket}[1]{\ensuremath{\left\vert #1 \right\rangle}}
\newcommand{\bra}[1]{\ensuremath{\left\langle{#1}\right\vert}}
\begin{document}
\Qcircuit@C=0.7em@R=0.7em {
\lstick{\ket{0}} &\gate{H} &\qw &\qw &\qw&\cdots&&\ctrl{7} &\qw&\multigate{4}{\mathcal{QFT}_{n}^{-1}}&\qw&\qw&\meter&\qw&\qw \\
\vdots & & & & & && & & & & &\vdots \\
\\
\lstick{\ket{0}} &\gate{H} &\qw &\ctrl{4} &\qw&\cdots&&\qw &\qw&\ghost{\mathcal{QFT}_{n}^{-1}} &\qw&\qw&\meter&\qw&\qw \\
\lstick{\ket{0}} &\gate{H} &\ctrl{3} &\qw &\qw&\cdots&&\qw &\qw&\ghost{\mathcal{QFT}_{n}^{-1}} &\qw&\qw&\meter&\qw&\qw \\
\\
\\
\lstick{\ket{\psi}}&\qw{/^{m}}&\gate{U^{2^{0}}}&\gate{U^{2^{1}}}&\qw&\cdots&&\gate{U^{2^{n-1}}}&\qw&\qw
}
\end{document}首先假设\(|\psi\rangle\)包含\(m\)个量子比特,上半部分初始为\(n\)个状态为\(|0\rangle\)的量子比特。
这\(n\)个量子比特分别经过H门后变为\(\frac{1}{\sqrt{2^{n}}}(|0\rangle+|1\rangle)^{\otimes n}\)。
对于\(U\)门,因为\(U|\psi\rangle=\exp(2\pi i\theta)|\psi\rangle\),所以\(U^{2^{j}}|\psi\rangle=U^{2^{j}-1}U|\psi\rangle=U^{2^{j}-1}e^{2\pi i\theta}|\psi\rangle=e^{2\pi i2^{j}\theta}|\psi\rangle\)。
当\(C-U^{2^{j}}\)作用在\(\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes|\psi\rangle\)上后,该量子态变为\(\frac{1}{\sqrt{2}}(|0\rangle\otimes|\psi\rangle+e^{2\pi i2^{j}\theta}|1\rangle|\psi\rangle)=\frac{1}{\sqrt{2}}(|0\rangle+e^{2\pi i2^{j}\theta}|1\rangle|)\otimes|\psi\rangle\)。
所以在这些\(C-U^{2^{j}}\)门作用完之后,前n个量子比特变为\(\frac{1}{\sqrt{2^{n}}}(|0\rangle+e^{2\pi i2^{n-1}\theta}|1\rangle|)\otimes\cdots\otimes(|0\rangle+e^{2\pi i2^{1}\theta}|1\rangle|)\otimes(|0\rangle+e^{2\pi i2^{0}\theta}|1\rangle|)=\frac{1}{\sqrt{2^{n}}}\sum_{k=0}^{2^{n}-1}\exp(2\pi i\theta k)|k\rangle\)。
对其运用逆QFT之后,变为\(\frac{1}{2^{n}}\sum_{j=0}^{2^{n}-1}\sum_{k=0}^{2^{n}-1}e^{2\pi i\theta k}e^{-2\pi i\theta k/2^{n}}|j\rangle=\sum_{j=0}^{2^{n}-1}(\frac{1}{2^{n}}\sum_{k=0}^{2^{n}-1}e^{-2\pi ik(j-2^{n}\theta)})|j\rangle\)。
整体的量子态在该量子线路作用完后变为:\(\sum_{j=0}^{2^{n}-1}(\frac{1}{2^{n}}\sum_{k=0}^{2^{n}-1}e^{-2\pi ik(j-2^{n}\theta)})|j\rangle\otimes|\psi\rangle\)。
当\(\theta\)可以用\(n\)位二进制来表示的时候,即\(\theta=0.\theta_{n-1}\theta_{n-2}\cdots\theta_{0}\),因为\(j\)取值从\(0\)到\(2^{n}-1\),所以\(\exists j,j=2^{n}\theta\),故该状态的系数为\(1\),其他状态的系数为\(0\)。所以前\(n\)个量子比特变为\(|j\rangle\),故对其测量即可得到\(j\),从而得到\(\theta\)。